この記事では、オプションのギリシャ指標の1つ、ローについて解説します。
ローは、オプション価格と金利の関係を数値化した指標です。
重要度は他のギリシャ指標より劣りますが、オプション取引をする上で押さえておくべき知識の1つになります。
ギリシャ指標のローとは?
ローは、無リスク金利(リスクフリーレート)の変化に対するオプション価格の感応度を数値化した指標です。
ロー
無リスク金利が1%変化したときに、オプション価格が何円変化するか
金利とオプション価格の関係は、次のようになります。
| コールオプションの価格 | プットオプションの価格 | |
|---|---|---|
| 金利上昇 | 増加 | 減少 |
| 金利低下 | 減少 | 増加 |
そのため、ローの符号はオプション取引の方法で以下のように異なります。
・コール買い:正
・コール売り:負
・プット買い:負
・プット売り:正
ローを使った計算
たとえば、ロー=0.2%で無リスク金利が1%→1.5%に上昇したとき、
コールオプション価格の上昇幅 = (1.5 - 1) × 0.2 = 0.1円
※他のギリシャ指標と同じように、ローを使った上の計算もIVや原資産価格など他の要素が一定であるという仮定を前提としています
ローの計算式
ローは、数学的には無リスク金利に関するオプション価格の1次導関数になります。
そのため、ローは次のように表されます。
ローの式
$$ロー = - \frac{∂ C}{∂ r}$$
∂:偏微分の記号 C:オプション価格 r:無リスク金利
オプション価格はブラック‐ショールズ方程式より、次のように表されるので、
これをrについて偏微分すると、ローの計算式は次のように表されます。
配当利回りqなし
$$セータ(call) = KTe^{-rT}N(d2)$$
$$セータ(put) = ‐KTe^{-rT}N(‐d2)$$
ローの見方
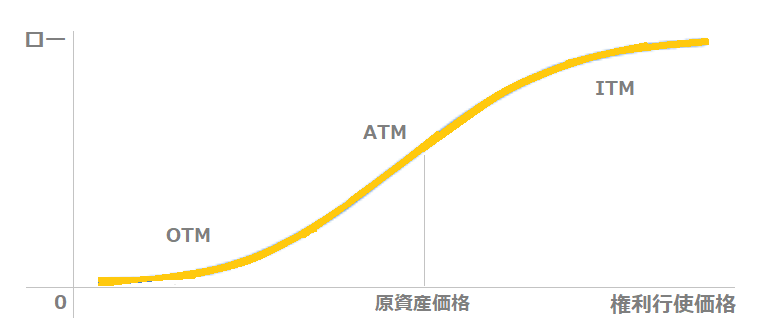
下の図は、コールオプションにおける「ロー-権利行使価格」のグラフです。
特徴
- 権利行使価格が高いほど、ローの数値は高くなる
- OTMが深くなるほど、ローは0へ向かって減少する
- ローの大きさ:ITM>ATM>OTM
深いOTMのコールオプションでは、無リスク金利による影響がとても小さいです。
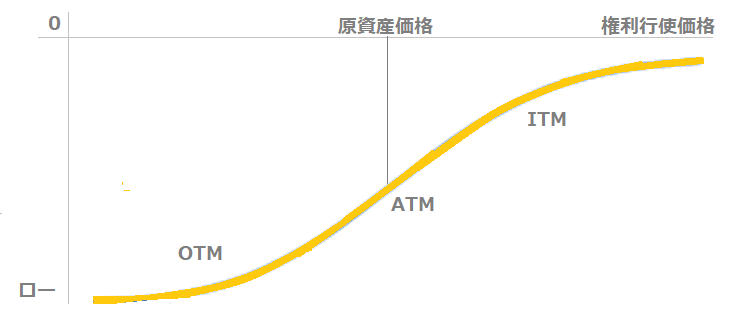
下の図はプットオプションにおける「ロー-権利行使価格」のグラフです。
特徴
- 権利行使価格に比例して、ローは上昇する
- ITMが深くなるほど、ローは0に向かって上昇する
- ローの大きさ(絶対値):OTM>ATM>ITM
コールオプションでは、権利行使価格が高くなるほど無リスク金利のオプション価格への影響度が高まりますが、
プットオプションでは、権利行使価格が低くなるほど無リスク金利の影響が高まります。
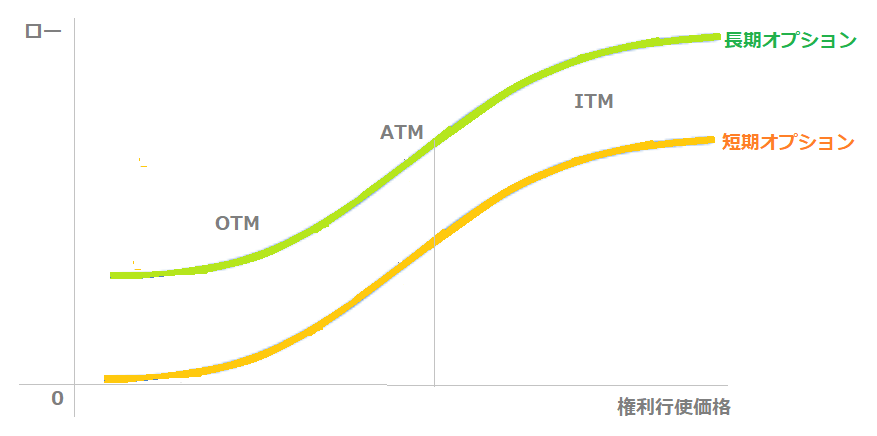
満期日までの残り日数が長いほどローの数値は大きくなるため、短期オプションよりも長期オプションに対する影響度のほうが大きいです。
ローは、オプション期間が長いほど増加し、満期日が近づくと0へと減少していきます。
※特に、「LWAPS」など残存期間が半年以上の長期オプションはローが注目されます。
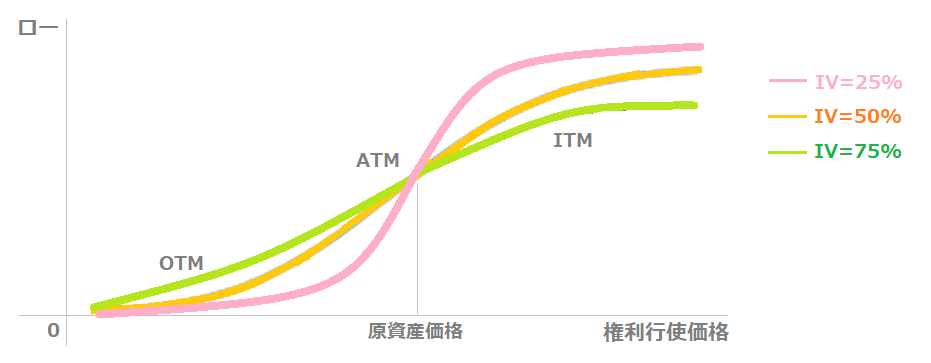
また、ローはインプライドボラティリティ(IV)によって大きさが変化します。
下の図は、IV=25%・50%・75%それぞれの「ロー-権利行使価格」のグラフです。
IVが高いオプションのロー
- ITMオプション:ローは低くなる
- ATMオプション:ローはほとんど変化しない
- OTMオプション:ローは高くなる
ローの影響度は?
ローはデルタやガンマ、セータなど、他のギリシャ指標とくらべてオプション価格への影響度ははるかに小さく、オプショントレーダーの中にはローをまったく意識していない方もいます。
基本的にはオプション取引で常にローを監視する必要はありませんが、FOMCの前後など金利が変更する可能性が高い場合はローの注目度が高まります。