この記事では、オプション取引におけるリスク指標の1つ「ベガ(vega)」を紹介します。
これはインプライドボラティリティ(IV)のオプション価格への影響度を測定する指標であり、IVを使う上で欠かさないものです。
【金融】ベガとは?【計算式】
オプション取引におけるベガ(vega)は、インプライドボラティリティ(IV)に対する、オプション価格の価格感応度を数値化した指標です。
具体的には、IVが1%変化したときの、オプション価格の変化量(〇〇円上昇/減少)を表します。
※IV=オプションの将来の予想変動率
→インプライドボラティリティとは?【見方&使い方を徹底解説!】
計算式
$$Vega=\frac{δC}{δσ}$$
※δC/δσ:σについての偏導関数 C:コールオプション価格 σ:インプライドボラティリティ
数学的には、σについて1回偏微分した一次偏導関数、つまりC‐σグラフの傾きになります。
オプション価格(C:コールオプション価格)は、ブラック‐ショールズ方程式より次のように表されるので、
これをσについて偏微分すると、Vegaの式は次のように表されます。
配当利回りなしのベガ
$$Vega=\frac{S\times\sqrt{T}\times e^{-\frac{(d1)^{2}}{2}}}{\sqrt{2\pi}}$$
配当利回りありのベガ
$$Vega=\frac{S\times\sqrt{T}\times e^{-(qT+\frac{(d1)^{2}}{2})}}{\sqrt{2\pi}}$$
ポイント
ベガは、コールオプション・プットオプション共に同じ数値になります。
そのため、上の式ではコールオプション価格(C)を使ってVegaを算出していますが、この数値はプットオプションのベガとしても利用できます。
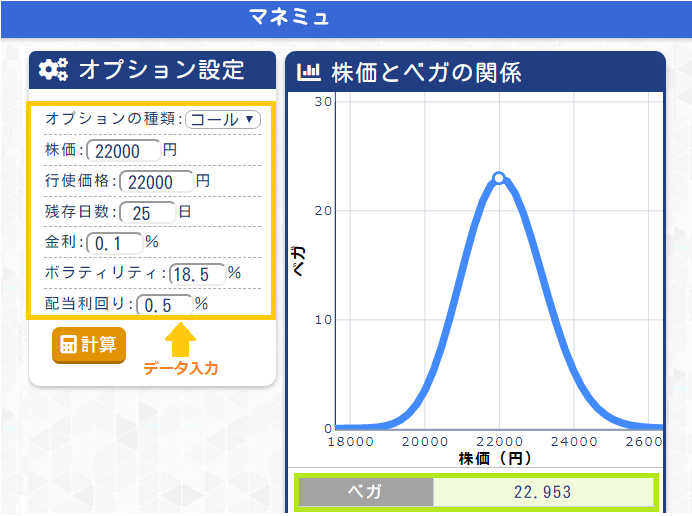
ベガの計算&グラフ作成サイトの紹介
ベガのデータは証券会社の取引ツールで確認できますが、他にも下記のサイトで簡単に計算することができます。
ベガを使った、オプションの価格変動幅の計算方法
オプション取引では一般的に、ファンダメンタルの悪化や株式ニュースなどで相場の先行きが不安定になると、IVが増加しオプション買いの需要が高まります。
このとき、IVの増加により理論上価格が何円動くかを、ベガを使って算出することができます。
計算式
オプション価格の変化量 = Vega × IVの変化量
計算例1
vega=3.0、現在のオプション価格=110円でIVが25%から26%まで上昇した場合、
価格の変化量=3.0 × (26-25) = 3.0 円
つまり、IVが1%上昇すると、オプション価格は理論上3円上昇して113円に到達します。
計算例2
vega=3.0、現在のオプション価格=110円でIVが25%から22%まで減少した場合、
価格の変化量=3.0 × (22-25) = -9.0 円
つまり、IVが3%減少すると、オプション価格は理論上9円減少して107円まで低くなります。
ポイント
・vegaが小さい:インプライドボラティリティのオプション価格への影響度小
→保有オプションのボラティリティ変動によるリスク小
・vegaが大きい:インプライドボラティリティのオプション価格への影響度大
→保有オプションのボラティリティ変動によるリスク大
グラフで見る、ベガに影響を与える5つの要因
次の5つは、ベガの数値に影響を与える要因です。
- 満期日までの残り日数
- 有効期限
- オプションの期限
- 原資産価格
- インプライドボラティリティ
それぞれのベガとの関係性を、順にグラフで見てみましょう。
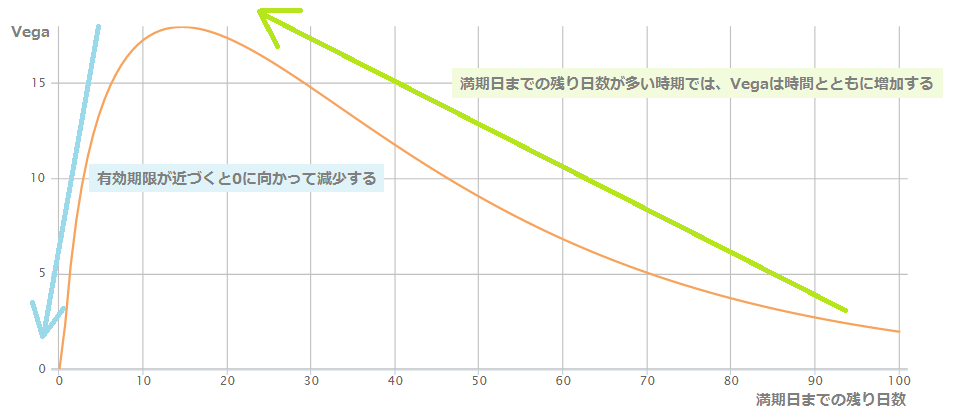
満期日までの残り日数とベガの関係
ベガはオプション価格と同じように、時間の経過(満期日までの残り日数)とともに数値が変化します。
上の画像は、「縦軸:Vega、横軸:満期日までの残り日数」のグラフです。
満期日までの残り日数が多い時期では、Vegaは時間とともに増加しますが、有効期限が近づくと減少し、最終的に0になります。
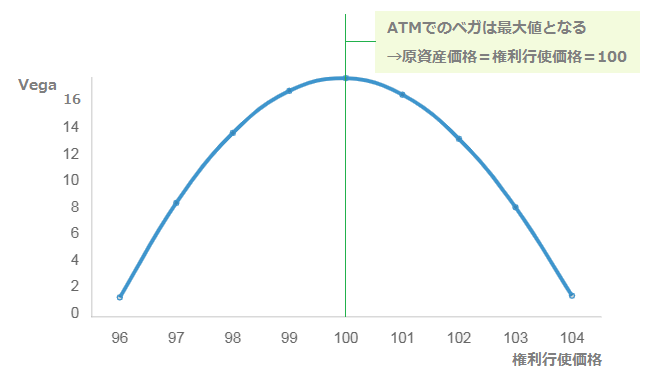
権利行使価格とベガの関係
権利行使価格の「IVの変化に対する感応度」は、価格に応じて異なります。
原資産価格に近い行使価格のオプションはIVの変化に敏感ですが、イン・ザ・マネー(ITM)やアウト・オブ・マネー(OTM)のオプションはIVの影響を受けにくいです。
上の画像は、「原資産価格=100円での縦軸:Vega,横軸:権利行使価格」のグラフです。
アット・ザ・マネー(ATM)のとき、ベガは最大値をとります。
そして、権利行使価格が現在の原資産価格から近いほどベガは増加し、権利行使価格が現在の原資産価格から離れるほどベガは減少します。
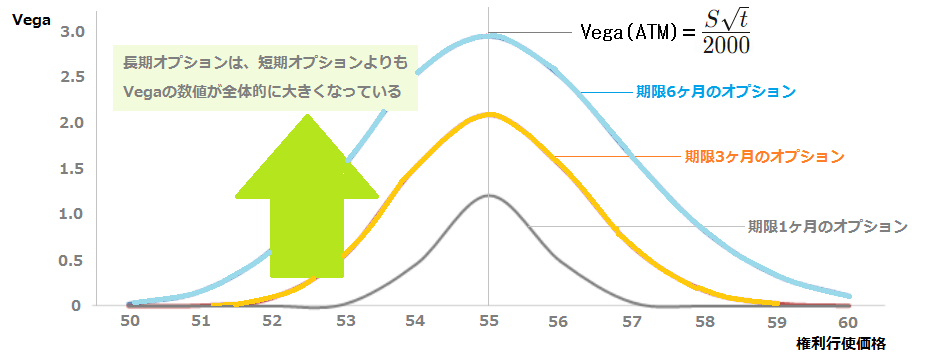
オプションの期限とベカの関係
一般的に、短期オプションはインプライドボラティリティの影響を受けにくく、長期オプションはより影響を受けやすいです。
そのため、長期オプションはIVの変化に対して、価格がより大きく動く傾向があります。
上の画像は、「期限1ヶ月・3ヶ月・6ヶ月の各オプションそれぞれの、Vega‐権利行使価格」のグラフです。
長期オプションは、短期オプションよりもVegaの数値が全体的に大きくなっています。
Vega(ATM)
アット・ザ・マネー(ATM)におけるベガは、次の式で表されます。
$$Vega=\frac{S\times\sqrt{T}}{2000}$$
この式より、ATMにおけるVega(上のグラフの頂点)は、「S:原資産価格」と「T:満期日までの日数」に比例して大きくなります。
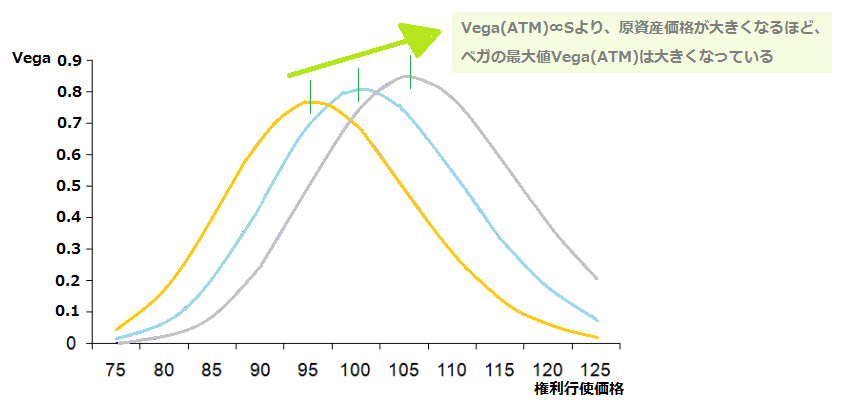
原資産価格とベガの関係
上のVega(ATM)の式で見たように、ATMにおけるベガの数値は原資産価格に比例します。
そのため、下のグラフのように、原資産価格が大きくなる(グラフが右にシフトする)ほど、ベガの最大値は大きくなります。
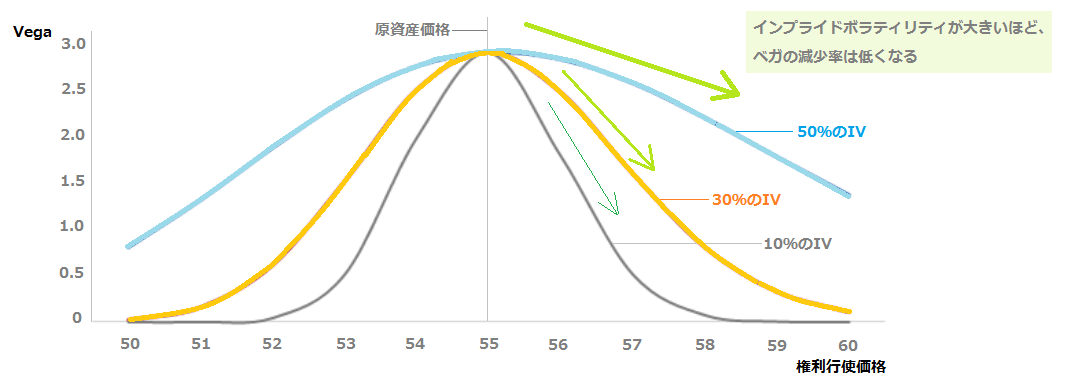
インプライドボラティリティの大きさとベガの関係
上の画像は、「10%・30%・50%のIVそれぞれの、Vega‐権利行使価格」のグラフです。
インプライドボラティリティが大きいほど、行使価格が原資産価格から離れたときのベガの減少率は低くなります。
また、アット・ザ・マネー(ATM)のオプションのベガは、IVの大きさに関わらずただ1つの数値になっています。