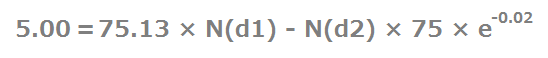この記事では、インプライドボラティリティ(IV)について解説します。
これはオプション価格が今後どれだけ変動するかを予測するボラティリティ指標で、オプショントレーダーにとって最も重要な指標の1つになります。
満期日までに相場が特定の価格に達する確率を確認でき、オプション取引で利益を上げるために必須のツールです!
目次
インプライドボラティリティとは?
インプライドボラティリティ(IV)とは、オプション取引における相場の将来のボラティリティ(価格変動率)の推定値を算出する指標です。
オプショントレーダーはインプライドボラティリティを利用して、オプション価格が特定期間にどれだけ動く可能性が高いか予測して取引します。
詳しくは、『はじめてのオプション取引|楽天証券』を参考にしてください。
IVはオプション価格に影響を与える要因
オプション価格はブラック-ショールズ方程式によって価格設定されますが、インプライドボラティリティはこの式の変数の1つです。
つまり、IVはオプションの価格を決める要因の1つになります。
ブラック-ショールズ方程式は次のとおりです。
関連 ブラック-ショールズ方程式とは?|ASSET NOTES
インプライドボラティリティが高くなるのは、将来の価格変動率の期待値が大きいということであり、オプション買いで大きな利益を上げる可能性が高いです。
そのため、IVが上昇したオプションは人気が集まり、新規買いにより価格が上昇しやすいです。
- IVの数値が高くなる → オプション価格上昇
- IVの数値が下がる → オプション価格下落
また、株価(原資産価格)とIVの間には、負の相関関係があります。
- 株価上昇 → 保有株の値下がりリスクに対するヘッジ需要が低下し、IVは低下する
- 株価下落 → 保有株の値上がりリスクをヘッジする、プットオプション買いの需要が高まり、IVは増加する
逆に、IVが高まってくると、投資家の不安心理を煽ってリスクオフの動きが強まり、株価の下落を引き起こします。
ベガの紹介
インプライドボラティリティのオプション価格への影響度は、権利行使期間満了までの残り時間に依存します。
時間が短いほど、IVが価格に与える影響は小さくなります。
このオプション価格のIVに対する感応度は、ベガ(vega)という指標で数値化されます。
詳しくは→ オプション取引のベガとは?【計算式&グラフ】
IVの3つの長所
インプライドボラティリティを使うメリットは、次の3つがあります。
IVのメリット
- 市場参加者のマーケットに対する市場心理(市場センチメント)や相場のリスクの度合いを定量化
- オプション価格の価格設定に使われる→IVはオプション価格の時間的価値に影響を与える
- 特定期間における相場の価格変動幅を確率で算出できる
詳しくは、後ほど解説します。
※IVはギリシャ指標「デルタ・ガンマ・ベガ・セータ・ロー」の数値にも影響を与えます。
インプライドボラティリティの計算式
インプライドボラティリティの数値は、オプション価格の計算に使われるブラック-ショールズ方程式を使って算出できます。
計算方法
step
1ブラック-ショールズ方程式に、IV以外のデータを入力
現在のオプション価格や行使価格、無リスク金利、満期までの時間などを式に代入します。
step
2試行錯誤法を使い、①で得られた式を満たすIVを探す
たとえば、データを入力した式が下記だとします。
N(d1)・N(2)内のσに適当な数値を入れて、上の式が成立するσの数値を探します。
※インプライドボラティリティの数値は、実際に計算する必要はありません。証券会社の取引画面で確認できます。
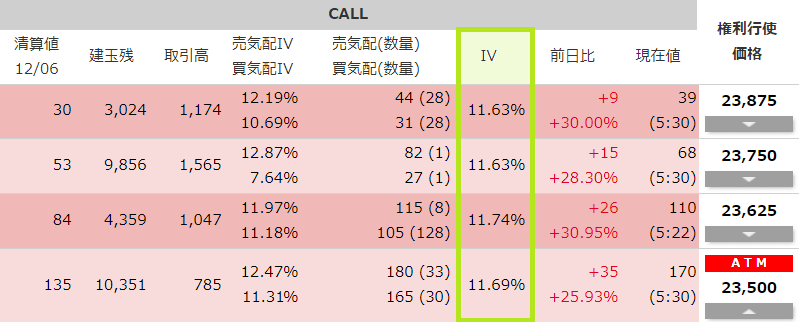
日経225オプションのIVデータ&チャート
日経225オプションのIVデータは、サイト「JPX日本取引所グループ」でCheckできます。
データの保管場所
マーケット情報→先物・オプション関連→オプション価格情報
また、日経225オプションのIVチャートは、サイト「オプション道場」で見ることができます。
IVを使った、価格の標準偏差の計算方法
インプライドボラティリティを使うことで、有効期限までのオプション価格の予想レンジ幅を標準偏差で算出することができます。
計算式
$$1σ(標準偏差)=オプション価格\times年次IV\times\sqrt{\frac{有効期限までの日数}{年間取引日数}}$$
計算例1
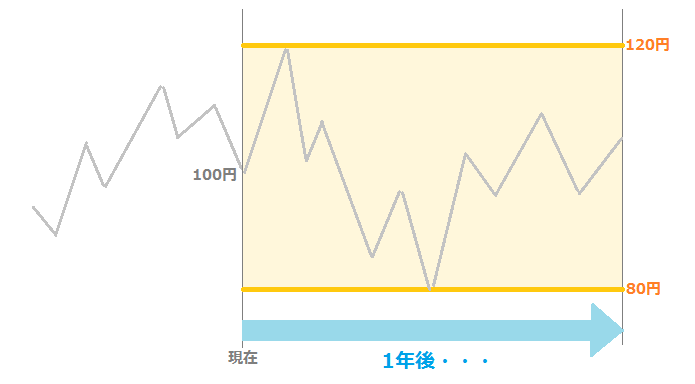
年次インプライドボラティリティ=20%、年間取引日数=245、現在の価格=100円の1年間の価格変動幅は、
$$1σ=100\times0.20\times\sqrt{\frac{245}{245}}=20円$$
「1σ=20円」は、1年間で価格が上下に20円動く確率(=80円~120円のレンジに収まる確率)が統計上68.27%であることを意味しています。
計算例2
年次IV=30%、現在の価格=100円の180日後(=満期までの日数)の予想変動幅は、
$$1σ=100\times0.30\times\sqrt{\frac{180}{245}}=25.7円$$
68.27%の確率でオプションの満期日までに、価格が74.3円~125.7円のレンジ内にとどまっていると予想できます。
また、標準偏差の2倍(2σ)も次のように計算できます。
計算例3
年次IV=20%、現在の価格=150円の年間予想変動幅(2σ)は、
$$2σ=1σ\times2=150\times0.20\times\sqrt{\frac{245}{245}}=60円$$
「2σ=60円」は、1年間で価格が90円~210円のレンジに収まる確率が統計上95.45%であることを意味しています。
注意点
この式で標準偏差を算出するとき、「満期日までの日数」に近い期間のインプライドボラティリティを使用してください。
たとえば、10日間の標準偏差を計算する場合は1ヶ月のIVデータを使い、290日間の標準偏差では年次IVを使います。
$$10日間の1σ(標準偏差)=オプション価格\times1ヶ月のIV\times\sqrt{\frac{10}{20}}$$
※1ヶ月の取引日数を20と仮定
遠い期間のIVを使うと、計算結果の精度が悪くなります。たとえば、20日間のσの計算に年次IVを使うのはおすすめできません。
1日の推定値幅の算出方法
インプライドボラティリティで1日の値幅(レンジ幅)の予測値を求めることができます。
計算式
$$1日の値幅(1σ)=前日の終値\times1ヶ月のIV\times\sqrt{\frac{1}{20}}$$
※1ヶ月の取引日数を20と仮定
計算例
前日の終値=112円、1ヶ月のIV=1%での1日の値幅は、
$$1σ=112\times0.01\times\sqrt{\frac{1}{20}}=0.25円(25pips)$$
つまり、1日の予測値幅(確率68.27%)は50pipsで、87円~137円の価格帯を上下動すると予測できます。
※年次IVでも求めることができますが、1ヶ月のIVと比べて予測値の信頼性は低くなります。
また、年次IVや月IVから「1日のヒストリカルボラティリティ」を擬似的に算出することもできます。
1日のIV
$$1日のIV=年次IV\times\sqrt{\frac{1}{245}}$$
$$1日のIV=1ヶ月のIV\times\sqrt{\frac{1}{20}}$$
たとえば「1日のIV=1.25 %」なら、統計上3日に2日(確率68%)、1日の値幅が-1.25%~1.25%の範囲に収まると予測されます。
また、取引日の95%以上の日が、‐2.5%~2.5%(‐2σ~2σ) の値幅内に収まると予測できます。
※1日の値幅は、ADR指標でも予想できます、詳しくは『1日の平均レンジ幅を予測するADRの使い方&見方』を参考にしてください。
インプライドボラティリティの変動要因
インプライドボラティリティに影響を与える要因は、次の3つがあります。
- 供給と需要のバランス
- 満期までの残存日数
- 相場の不確実性(ニュースや金融イベントなどのファンダメンタル)
1.供給と需要のバランス
供給と需要は、インプライドボラティリティの大きさを決める主な要因です。
供給と需要の均衡が崩れる(過剰な需要/供給)と、IVは大きく変動します。
・オプションの需要(買い)や市場の期待が高まる→価格は上昇する傾向があり、IVも上昇する
・オプションの需要が低下(または供給が低下)する→IVは減少する
2.満期までの残存日数
満期までの残存日数(期限切れになるまでの時間)もIVに影響を与えます。
・残存日数が少ないオプションや短期オプション:IVが低くなりやすい
・残存日数が多いオプションや長期オプション:IVが高くなりやすい
3.相場の不確実性
オプション取引はリスクヘッジの役割もある金融商品です。
相場の将来の動向が不透明になると、資産の値下がりリスクを回避するためにオプションの需要が高まり、IVが上昇します。
逆に、相場の不確実性が解消されると、オプション価格が下がりIVも低下します。
相場の不確実性(リスクの高まり)は、金融イベントや会社の関連ニュースによって引き起こされます。
金融イベント例:政策金利発表・アメリカ大統領選挙・FOMC
会社のニュース例:四半期決算発表・M&A
市場参加者はイベントやニュースの前に期待や予想で行動するため、一般的にイベントやニュースの発表に先立ってIVは増加し、発表後IVは大きく減少する傾向があります
インプライドボラティリティチャートの分析
インプライドボラティリティチャートは、現在のIVと過去のIVの数値を比較したり、IVの推移を把握するのに役立ちます。
※IVチャートは、証券会社のIVヒストリカルデータを使って作成することができます
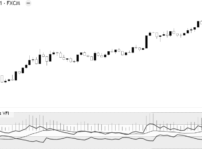
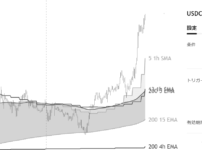
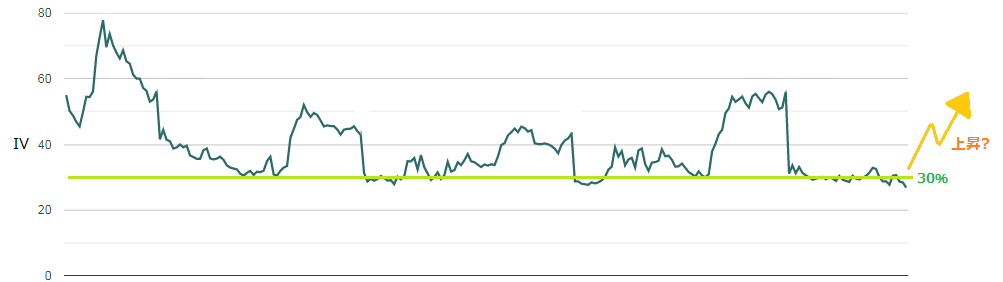
下のチャートは、ネットフリックスの1年間のIVチャートです。
直近のIVの数値と比較すると、現在のIV(26.8%)は相対的に低い数値であるとわかります。
また、この1年間で30%の水準が最低水準となっており、IVは今後上昇する可能性が高いと予想できます。
基本戦略1
IVが相対的に低い場合:将来のボラティリティの増加を期待して、長期オプション買いが有効
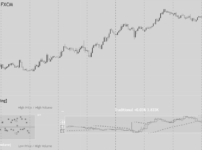
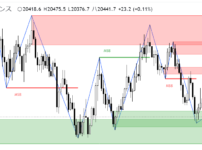
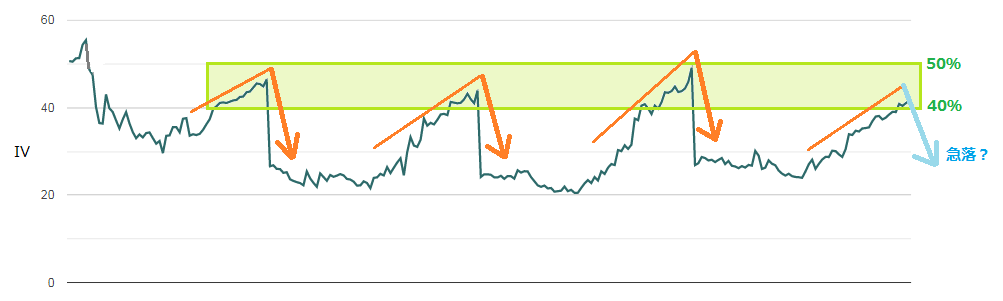
上のIVチャートでは、現在のIV(41.6%)が高値圏40%~50%にあり、相対的に高い水準にあるとわかります。
また、過去の動きを見ると、IVは高値圏まで上昇すると大きく急落するパターンが繰り返されています。そのため、今回も大きな下落が生じる可能性が高いです。
基本戦略2
IVが相対的に高い場合:オプション価格は高騰しており、オプション売りが有効
IVのサイクルレンジと平均値回帰
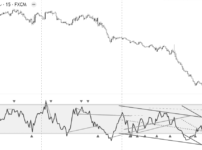
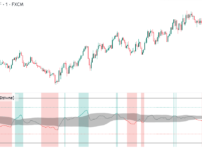
インプライドボラティリティは、特定のレンジ内で周期的に上下動して、高ボラ/低ボラを繰り返すことがあります。
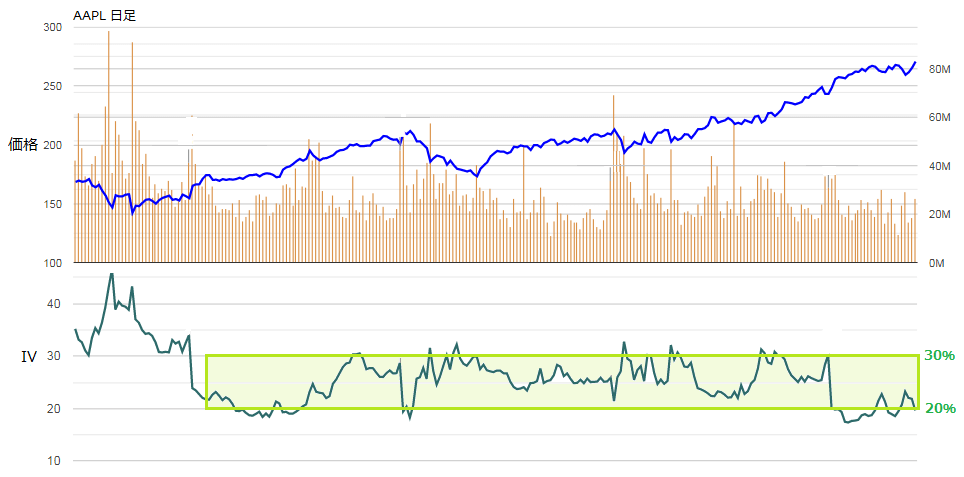
上のアップル日足チャートでは、IVが20%~30%の水準でレンジを形成しています。
・20%:レンジの下限。相対的な低ボラテリティ水準
・30%:レンジの上限。相対的な高ボラテリティ水準
20%や30%に到達すると、IVは平均値25%に回帰する傾向があります。
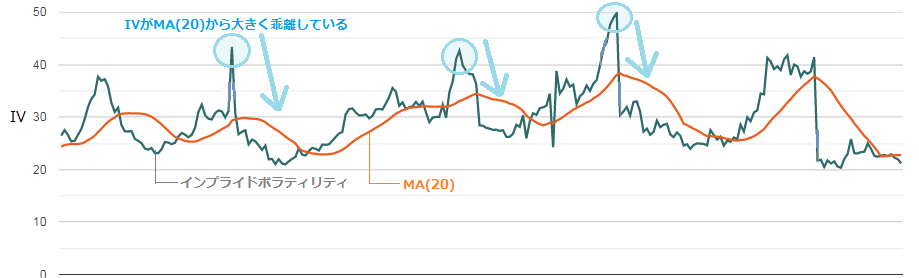
また、IVが移動平均線から大きく乖離するのは、ボラティリティが極端に増加/減少していることを示唆しており、MA(=IVの平均値)に回帰すると予測されます。
相対的なインプライドボラティリティの評価【各銘柄のIVの比較】
異なるオプション銘柄は、それぞれ独自のインプライドボラティリティをもっています。
そのためIVの欠点として、異なる銘柄のIVの大きさを比較して、どちらがボラテリイティが大きいが判定することはできません。
たとえば、銘柄AのIVが30%、銘柄BのIVが25%の場合、単純に銘柄AのボラがBより大きいとは限りません
※相対的なIVの大きさを評価する指標に、「IVランク」と「IVパーセンタイル」があります。詳しくは、下の記事で解説しているので、ぜひ参考にしてください。
インプライドボラティリティを異なる銘柄で比較できる指標 IVR&IVPとは?
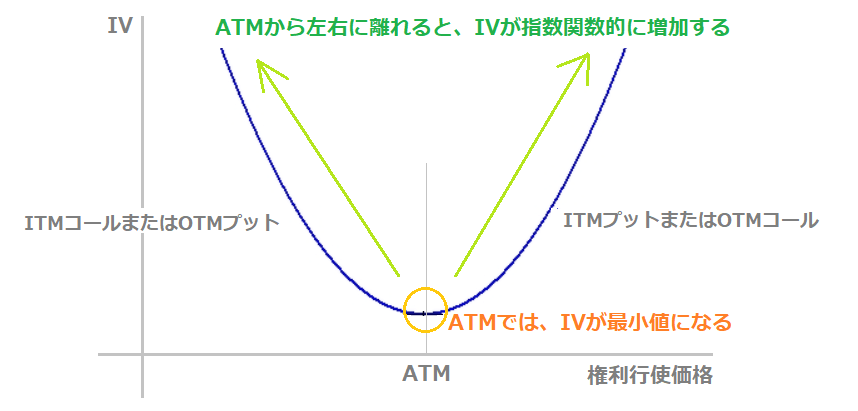
※また、各権利行使価格におけるオプションのIVの大小関係は、「スマイルカーブ」というグラフで簡単に見ることができます。
詳しくは→ 【オプション】スマイルカーブの使い方&見方
ヒストリカルボラティリティとの違い【HV&IVの比較分析】
オプションのボラティリティを測定する指標には、ヒストリカルボラティリティ(HV)もあります。
HVとIVの違いは、つぎのとおりです。
HVの特徴
- 過去のボラティリティと比べた、現在のボラティリティを標準偏差で表した統計的指標
- 他の銘柄のHVと比較することも可能
- 実際の価格変動幅から算出される
- HVの数値は、「現在」のボラテリティの実際の大きさを表す
- 過去のHVの数値は、過去の実際のボラティリティである
IVの特徴
- IVの数値は、「将来」のボラティリティの推定値を表す
- オプション価格や行使価格などのデータから算出される→過去の価格変動幅の数値は、計算式に含まれていない
- 他の銘柄のIVと比較できない→IVランクやIVパーセンタイルで代用可能
- 過去の数値は、過去のボラティリティを表していない→過去のIVは、その時点での将来のボラの推定値にすぎない
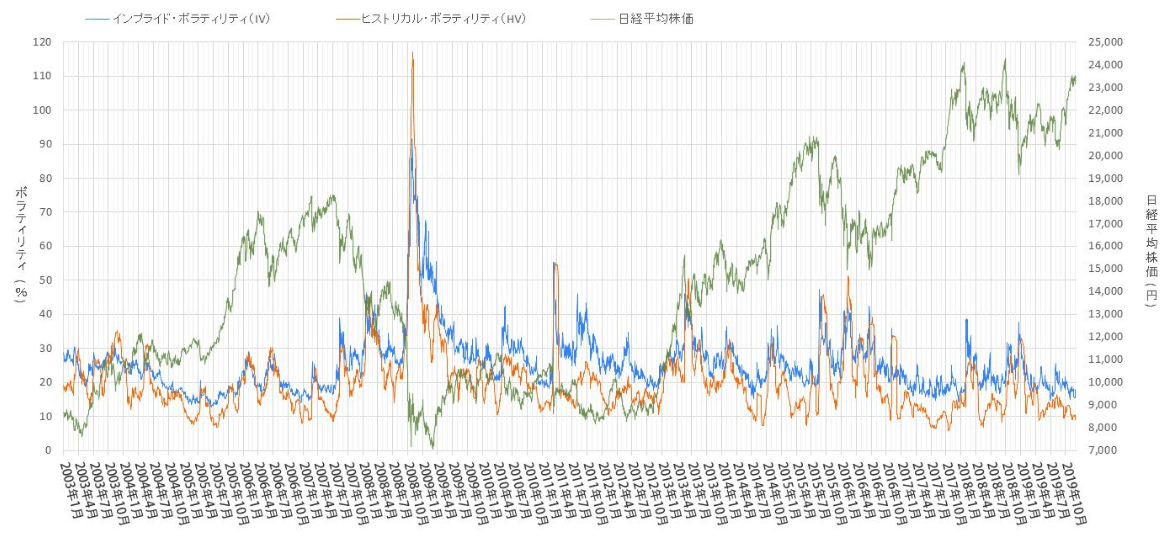
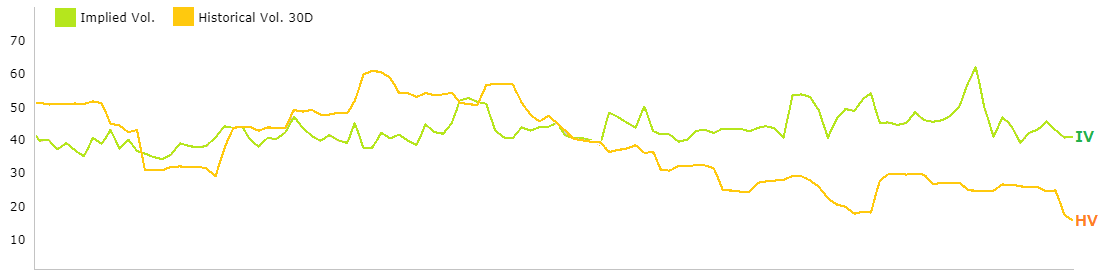
HV&IVの比較分析
インプライドボラティリティとヒストリカルボラティリティを比較して、そのオプション銘柄が過大評価/過小評価されているかを調べることができます。
IVが低いオプションは注目度が低く、割安なオプションと考えられます。
オプションのボラはこれから平均値まで上昇する可能性が高いため、オプション買いが有効です。
早い段階でオプションを購入することで、大きな利益が得られるチャンスになります。
オプション価格が割高であるため、オプション買いはリスクが高く、売りが有利な状況です。
過熱したIVは平均値まで回帰して、相場のボラティリティが下がる可能性が高いです。
注意点
IVとHVを比較する時は、互いの期間がかけ離れていないデータを利用してください。
たとえば、満期日が2ヶ月のオプションのIVでは、期間40(1ヶ月の平均取引日20×2)のHVと比較分析します。