ヒストリカルボラティリティというテクニカル指標をご存知ですか?
これは、FXや株の相場のボラティリティを測定する指標で、ヘッジファンドや機関投資家が注目している指標の1つになります。
この記事では、ヒストリカルボラティリティに関する下記の7つの項目を解説します。
目次
ヒストリカルボラティリティとは
ヒストリカルボラティリティ(HV)は、為替レートや株価の変動幅が、過去の特定期間における平均値からどれだけ乖離しているか計算し、過去の価格の変動率を測定する指標です。
ヒストリカルボラティリティを利用することで、現在の相場のボラの大きさを把握したり、潜在的なリスクの度合いを評価することができます。
HVの見方
一般的に、HVの数値が大きいほど価格が短期間で一方向に急激に動く可能性があり、大きな損失が被るリスクがあります。
逆にHVの数値が低いと、価格の動きは緩やかで変動幅が小さい相場になります。
HV
- HVの数値高い:ボラ高い→リスク大
- HVの数値低い:ボラ低い→リスク小
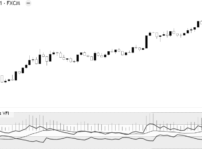
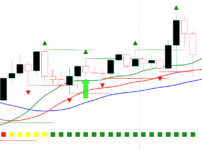
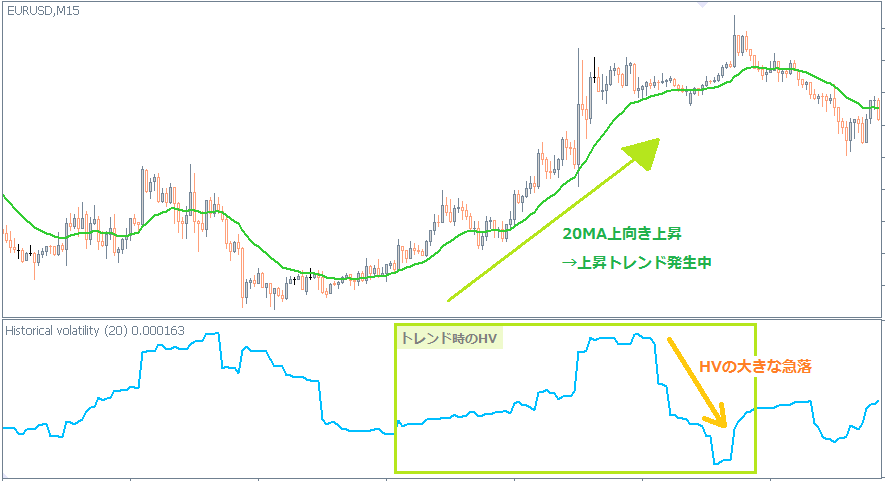
上のユーロドル15分足では、期間20のヒストリカルボラティリティを表示しています。
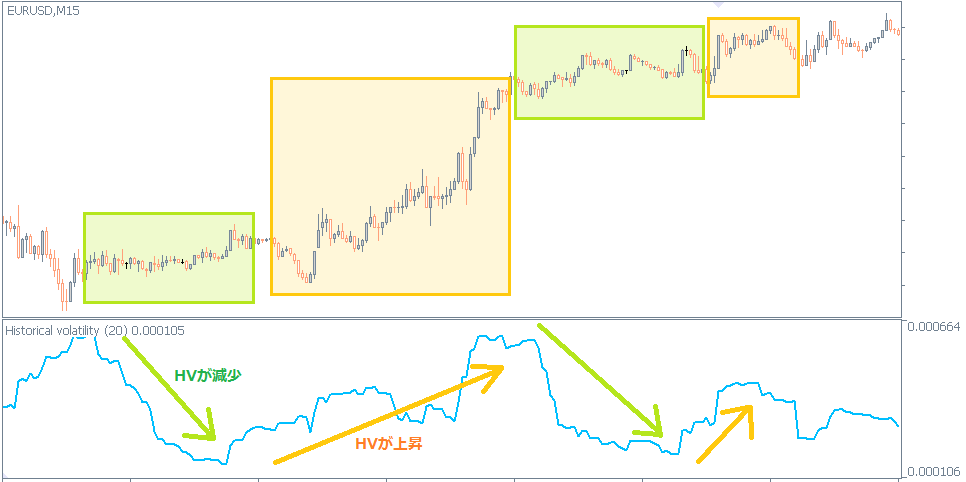
HVの上昇
相場のボラティリティが増加している
価格が上下に大きく動いており、上昇・下落の速度が速い
相場の進行・反転の変化が速いので、仕掛けや手仕舞いのタイミングが遅れないように気をつけましょう。
HVの減少
相場のボラテリティが低下している
閑散とした値動きが小さい相場で、リスクが小さいですが得られる利益も小さい
注意点
ヒストリカルボラティリティは、相場の方向性やトレンドの有無は測定できません。
あくまで相対的なボラの大きさを定量化する指標です。
そのため、移動平均線などのトレンド指標と併用することが推奨されています。
役割分担の例
- MAでトレンドの発生を発見
- HVでそのトレンドのボラティリティを分析
上のチャートのように、トレンド相場でのHVの大きな急落は、トレンドが終了する可能性が高いことを知らせる警告シグナルです。
ヒストリカルボラティリティの計算式
ヒストリカルボラティリティは、現在のボラティリティを価格変動率の標準偏差で算出します。
具体的な計算方法は、次のとおりです。
step
1終値の比の自然対数を計算
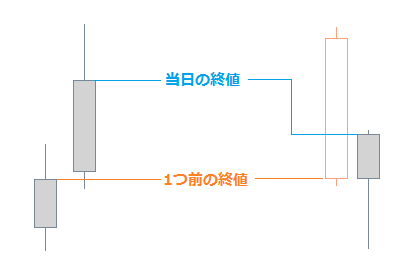
ヒストリカルボラティリティでは、当日のローソク足の終値と1つ前のローソク足の終値の比率を、価格の変動率として扱います。
まず、n本のローソク足それぞれにおいて、次の計算でVnを求めます。
Vnの定義
$$Vn=In \frac{Cn}{Cn‐1}$$
In:自然対数 Cn:終値 Cn-1:前の足の終値
n:ボラティリティーを調べる期間
日足の場合、Vnは前日の終値に対してどれくらい価格が1日で動いたか、1日の変動率を表します。
たとえば、前日の終値が100円で翌日の終値が110円の場合、
$$Vn=In \frac{110}{100}=0.0953$$
になります。この数値は、下の上昇率と近似した値になります。
$$上昇率=\frac{110-100}{100}=0.1$$
自然対数をとる理由
単純な終値の比では、同じ価格分上昇or下落しても、変化率の絶対値が同じにならず比較しにくいです。
$$上昇=\frac{150}{100}=0.5 下落=\frac{100}{150}=0.67$$
そこで、この比率の自然対数を求めてみると、次のように上昇率と下落率の絶対値が同じになり、比較しやすくなっています。
$$Vn=In \frac{150}{100}≒0.41 Vn=In \frac{100}{150}≒-0.41$$
このように、自然対数をとることで、上昇率と下落率が対称になります。
※詳しく学びたい方は、下記のサイトが参考になります。
step
2①で求めた各変動率の平均値を計算
各変動率(V1,V2,・・・Vn)の平均値V avgを次の式で求めます。
平均値V avg
$$V avg=\frac{V1+V2+・・・+Vn}{n}$$
たとえば次のデータでは、V avgは0.26になります。
n=5:V1=0.2 V2=0.1 V3=0.4 V4=0.5 V5=0.1
$$→V avg=\frac{0.2+0.1+0.4+0.5+0.1}{5} =0.26$$
step
3①②より、標準偏差を計算する
まず、次の式で分散(Vnの散らばり度合い)を計算します。
分散
$$σ^2=\frac{\sum_{i=1}^{n}(Vi-V avg) ^2}{n-1}$$
Vi-V avg:平均からの偏差
そして、分散から平方根を取ると標準偏差になります。この標準偏差がヒストリカルボラティリティになります。
ヒストリカルボラテリティHV
$$HV=σ=\sqrt{\frac{\sum_{i=1}^{n}(Vi-V avg) ^2}{n-1}}$$
※上の式では、母集団ではなく標本の標準偏差を計算しているため、nではなく「n-1」で割っています。
この理由については、下記サイトで詳しく解説されているので参考にしてください。
不偏標本分散の意味とn-1で割ることの証明|数学の美しい物語
ヒストリカルボラティリティのおすすめ時間足&期間
ヒストリカルボラティリティは、主に日足・週足・月足の時間足で利用されます。
HVの時間足
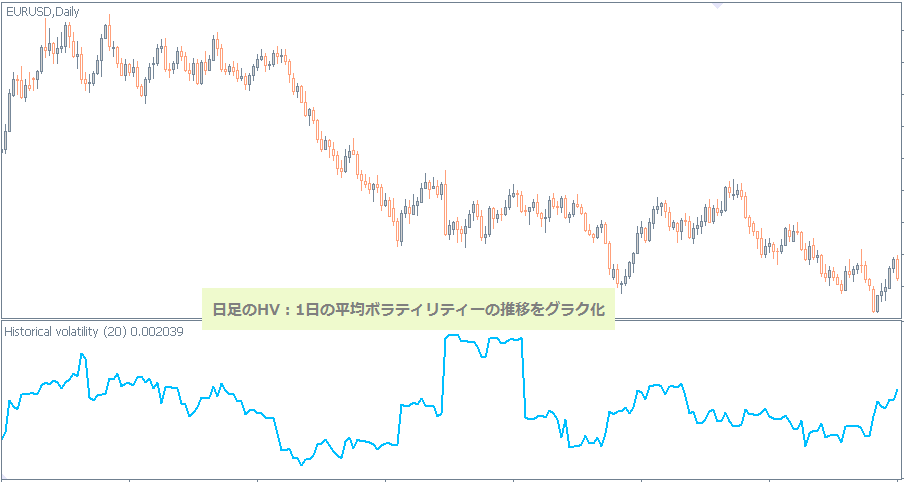
- 日足のHV:過去n日間における「1日」の平均ボラ
- 週足のHV:過去n週間における「1週間」の平均ボラ
- 月足のHV:過去nヶ月における「1ヶ月」の平均ボラ
大きな時間足のHVを見ることで、相場のボラティリティのサイクル(ボラの拡大・縮小の周期)を把握したり、近い将来のボラの状態を予測するのに役立ちます。
HVの期間のおすすめは?
FXでのHVパラメーターは、20期間が一般的です。
日足のHV(20)では、1ヶ月の平均取引日に相当し、1ヶ月(中期)のボラティリティーの推移を表します。
他には、長期のボラティリティを調べるのに、40・60・120・240などが使われます。これらはそれぞれ、2ヶ月・3ヶ月・6ヶ月・1年の平均ボラに相当します。
※株式相場では、25・50・75・150・300のパラメーターが使われます。
注意点
データの期間が多いほど精度が高くなりますが、ボラティリティは時間の経過とともに変化するため、古いデータは現在のボラを把握する妨げの要因になります。
そのため、現在のボラテリティの傾向を厳密に分析したい場合は、短期的なボラティリティを計測する「期間5・10」のHVがおすすめです。
ただし、パラメーターが小さいほど、ノイズが混ざりやすくなることに注意してください。
※TradingViewのチャートでヒストリカルボラテリティやHVレシオを表示することができます
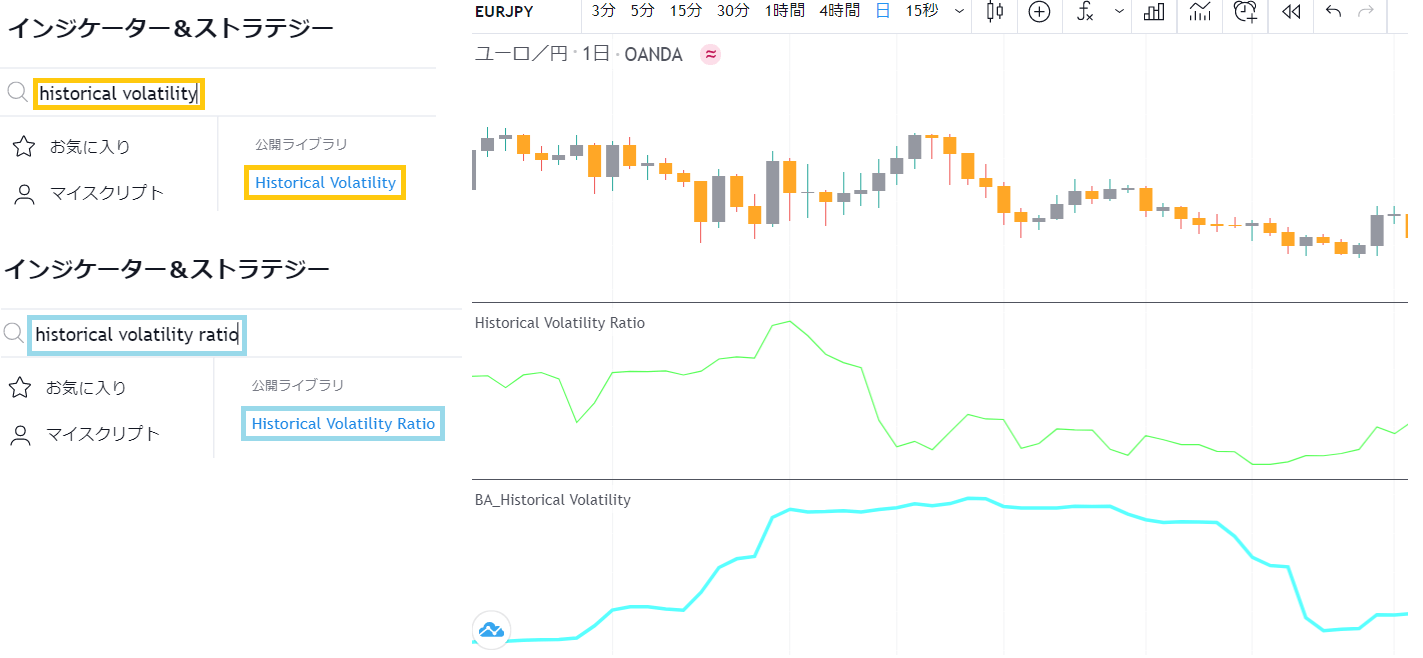
表示方法
インジケーター検索欄で「historical volatility」または「historical volatility ratio」と入力してクリックする
EMA式HVとHighLow-HV
通常のヒストリカルボラティリティでは、上の計算式②で見たように、各変動率(V1,V2,V3,・・・Vn)は平均値を算出するときに重みが同じです。
$$V avg=\frac{\sum_{i=1}^{n}Vi}{n}=\frac{V1}{n}+\frac{V2}{n}+ \frac{V3}{n}+・・・\frac{Vn}{n} $$
この計算式だと、古いデータと新しいデータが同格に扱われるため、最新のボラをより精確に測定するのに向いていません。
その欠点を克服するために開発されたのが、EMAヒストリカルボラティリティです。
これは直近のVnの値に大きな重みを与えて、古いデータは指数関数的に重みを減らすために、EMA(指数平滑移動平均)を式②に導入しています。
1日目のEMA‐HV
$$EMA‐HV=σ=\sqrt{\frac{\sum_{i=1}^{n}(Vi-V avg) ^2}{n-1}}$$
2日目以降のEMA‐HV
$$EMA‐HV=前日のEMA‐HV×(1-α)+Vn×α$$
EMA-HV:EMAヒストリカルボラティリティ
α:平滑化定数=2/(n+1)
※EMAの計算式については、「EMA|Money Partners」を参考にしてください
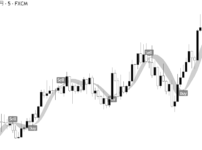
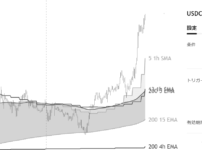
下のチャートでは、EMA式HVとSMA式HV(通常版)の2つを表示しています。
EMA式HVの方が、直近のボラの拡大・減少を素速く捉えています。
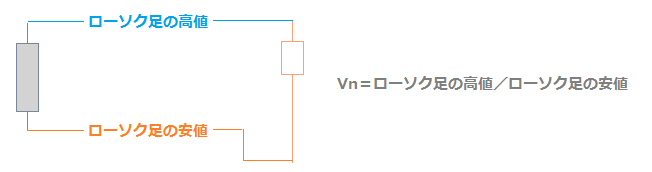
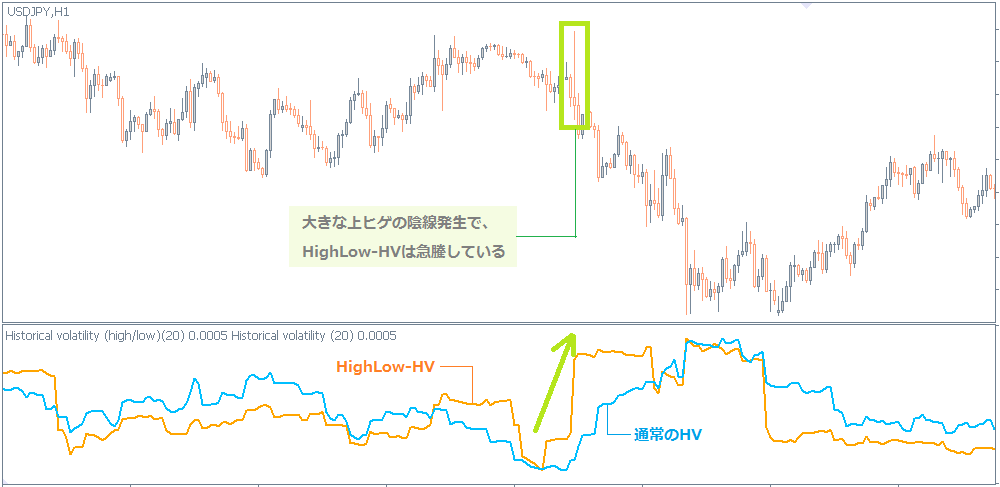
他にも、終値の比ではなく、ローソク足の高値と安値の比をVnとするバージョン「ハイローHV」もあります。
通常のHVでは、ローソク足のヒゲの大きさはボラティリティに反映されていません。ヒゲの大きさもボラテリティとして考慮したい場合はハイローHVがおすすめです。
これらのMT4・MT5インジケーターは、『【MT4・MT5】ヒストリカルボラテリティのインジケーター6選』で紹介しています。
HVの高ボラ水準の特定方法
ヒストリカルボラティリティが次のいずれかの条件を満たすとき、相場はボラティリティーは非常に高い状態にあります。
大きな価格変動に備え、損切幅を広くし、また損失を抑えるためにロット数(取引枚数)を通常より小さくしましょう。
- HVに表示したボリンジャーバンドがエクスパンション状態
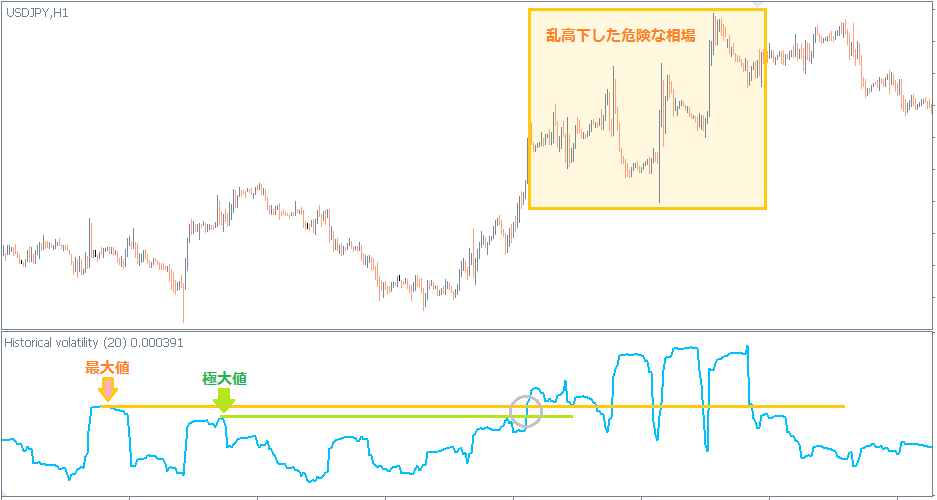
- 直近の最大値や極大値の水準をHVが超える
最大値や極大値を調べる範囲の目安
5分足:2~3日間 1時間足:10日間 日足:6ヶ月~1年 週足:2年~3年
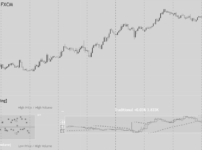
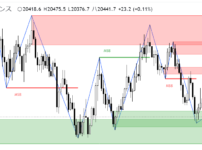
上のドル円1時間足では、最大値の水準を超えると価格が乱高下した危険な相場になっています。
ボリンジャーバンドがエクスパンションし、HVが+2σに沿って急騰している相場もリスクの高い相場になります。
※ボラティリティ指標に表示したボリンジャーバンドを使った「ボラティリティ分析」の詳細は、『相場のボラティリティを解析!ATRボリンジャーの使い方』で解説しています。
HVの銘柄スクリーニングサイト
ヒストリカルボラテリティを利用した「株の銘柄スクリーニング」は、下記のサイトで行えます。
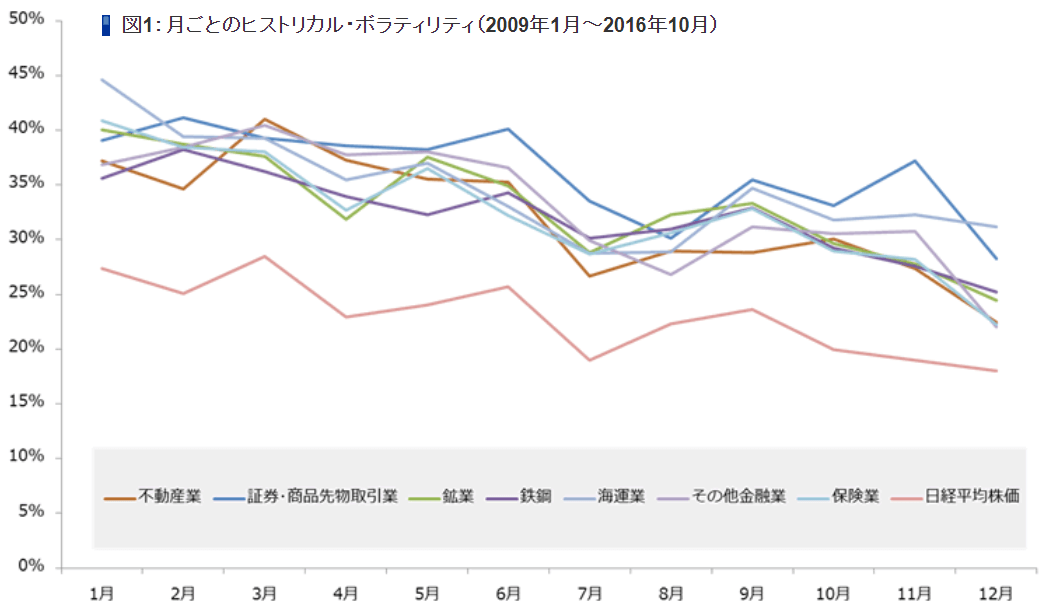
ちなみに、業種別の月ごとのHV(2009年1月~2016年10月)は次の通りです。
ヒストリカルボラティリティバンド
ヒストリカルボラティリティバンドは、移動平均線の上下に、HVの数値分離れた位置にバンドを表示する指標です。
HVバンド
- 上のバンド:SMA(20期間) + 2×HV
- 下のバンド:SMA(20期間) - 2×HV
これはボリンジャーバンドのように、バンドの幅でボラティリティーの状態を把握することができます。
HVバンド
・バンド幅の拡大:HVの値が上昇→ボラテリティ大
・バンド幅の縮小:HVの値が減少→ボラテリティ小
上のチャートのように、ローソク足がバンド外に飛び出すのは、トレンドやブレイクアウトの発生シグナルになります。
HVレシオ
HVレシオ(HV-Ratio)は、短期と長期の2つ期間のHVの比率を表示する指標です。
計算式
HV-Ratio = 短期 HV ÷ 長期 HV
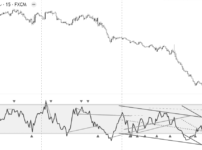
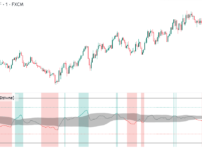
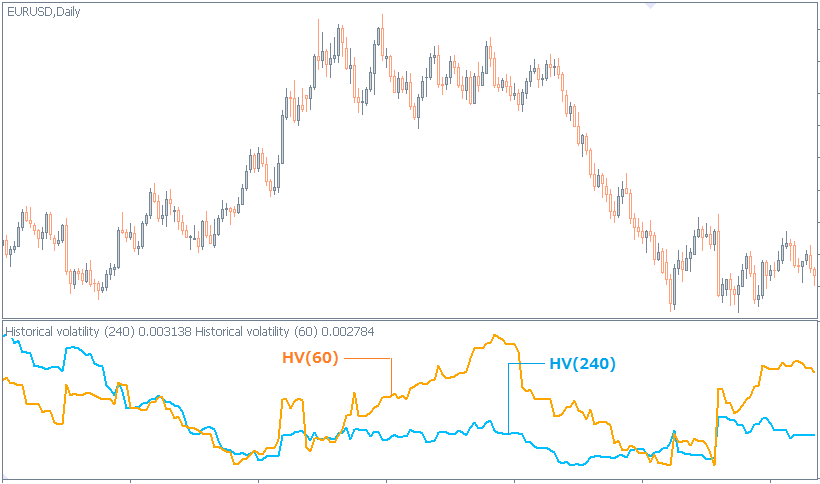
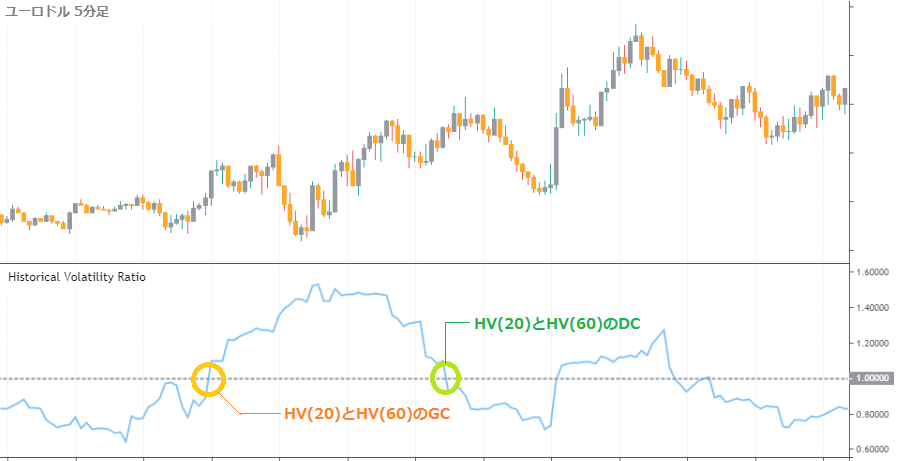
下のチャートのHV-Ratioでは、20期間のHVと60期間のHVの比を表しています。
HV-Ratioと1の水準とのクロスの位置関係は、次の通りです。
- HV-Ratio=1:HV(20)とHV(60)のクロス
- HV-Ratio>1:HV(20)がHV(60)の上で推移
- HV-Ratio<1:HV(20)がHV(60)の下で推移
HV-Ratioのクロス
- 1.0の水準をHV-Ratioが下から上に超える:HV(20)とHV(60)のゴールデンクロス
→短期のボラティリティが増加しているシグナル - 1.0の水準を上から下に超える:HV(20)とHV(60)のデッドクロス
→短期のボラティリティが減少しているシグナル
また、HV-Ratioは1.0を中心に0.5~2.0の範囲を上下動し、0.5と1.5の水準が注目すべき水準になります。
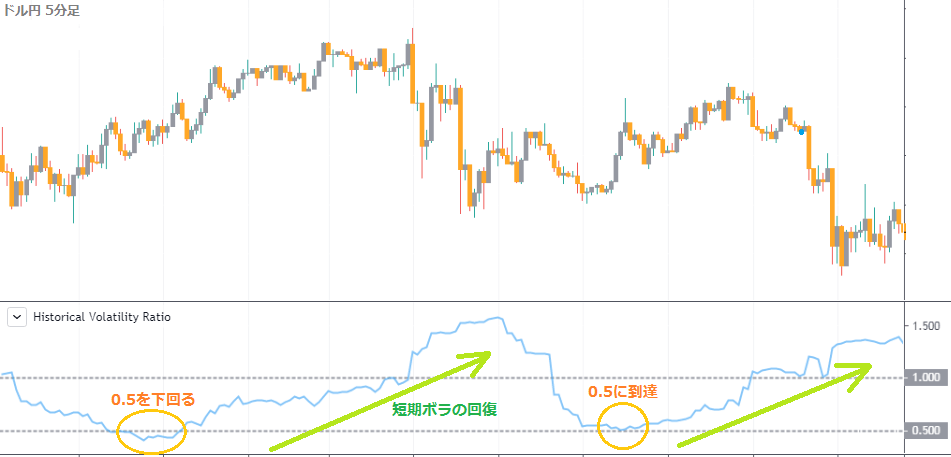
HV-Ratioが0.5を下回る
短期ボラの数値が長期ボラに比べ大きく下回ると、その反動でボラティリティーが平均値まで回復し、値動きが活性化し始めます。
停滞していた相場のHV-Ratioが0.5を下回ったら、トレンドやブレイクアウトがそろそろ発生する前兆になります。
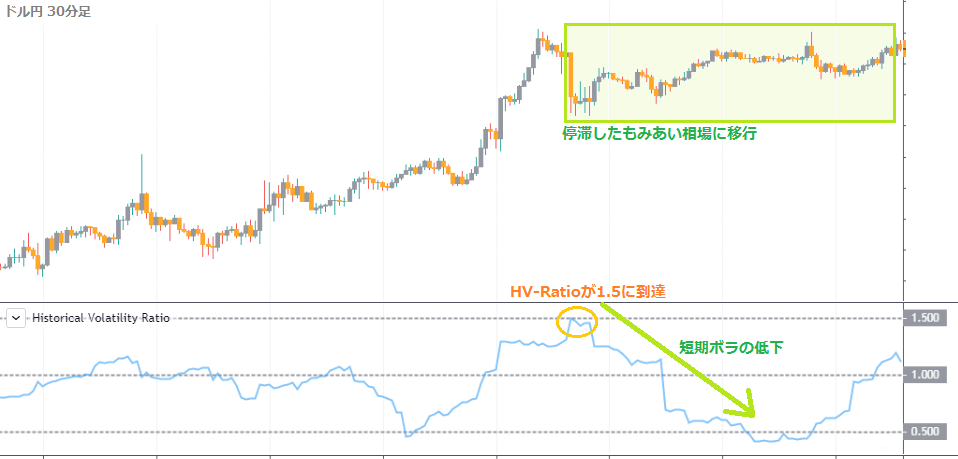
HV-Ratioが1.5を超える
HV-Ratioが1.5の水準を超える(または到達する)と、増加していた相場のボラティリティーは減少傾向に転換します。
トレンドやブレイクアウトは終了し、停滞したもみあい相場に移行する可能性が高いです。