この記事では、オプション取引におけるギリシャ指標の1つ「セータ」について解説します。
目次
【オプション】セータとは?
セータは、時間経過によりオプション価格がどれくらい低下するか、時間価値の減衰を数値化した指標です。
セータ
時間価値の減衰により、オプション価格が1日にどれだけ値下がりするか
オプションの買いでは、セータは通常負の数であり、オプションの売りでは、セータは正の数になります。
| オプションの種類 | セータの符号 |
|---|---|
| ロング・コール | 負 |
| ショート・コール | 正 |
| ロング・プット | 負 |
| ショート・プット | 正 |
セータの符号により、セータのオプション価格に与える影響は大きく異なります。
セータの符号
- 正:満期日が近づくにつれ、オプションの価値が上がる
- 負:満期日が近づくにつれ、オプションの価値が下がる
注意点
1つ注意点として、セータによるオプション価格の下落は、インプライドボラティリティや原資産価格などオプション価格に影響をあたるほかの要素がすべて一定であることを前提条件としています。
そのため、IVや原資産価格の上昇による価値の上昇が時間価値の減衰を上回った場合は、SQ日が近づいてもコールオプションの価格は上昇します。
時間価値の減少幅は、セータで計算できる!
セータを使って、n日後のオプションの推定価格を、次の式でもとめることができます。
計算式
現在のオプション価格 - 経過日数n × セータ
計算例
現在の価格が125円で、セータが-7円のコールオプションでは、
125 + 1 × (-7) = 118円
1日経過すると、理論上オプション価格は7円下落し、118円になると予測できます。※ただし、原資産価格やIVは一定とする
2日後では、
125 + 2 × (-7) = 111円
計算上、111円まで値下がりすると予測できます。
※後ほど詳しく解説しますが、セータは満期日が近づくほど絶対値が大きくなるので、2日後は111円より低くなります。
| 1日後 | 2日後 | 3日後 | 4日後 | |
|---|---|---|---|---|
| セータ値 | -7 | -7.3 | -7.8 | -8.7 |
| セータの変化 | -0.3 | -0.5 | -0.9 |
上の表のように、1日のセータによる価格の下落幅は日を追うごとに大きくなっていきます。
セータの計算式
セータは、満期日までの残り時間に対するオプション価格の1次導関数です。
そのため、セータは次のように表されます。
セータの式
$$セータ = - \frac{∂ C}{∂ T}$$
∂:偏微分の記号 C:オプション価格 T:SQ日までの残り時間
オプション価格はブラック‐ショールズ方程式より、次のように表されるので、
これをTについて偏微分すると、セータの計算式は次のように表されます。
配当利回りqあり
$$セータ(call) = -e^{-qt} \frac{SN(d1)σ}{2\sqrt{T}}-rKe^{-rt}N(d2)+qSe^{-qt}N(d1)$$
$$セータ(put) = -e^{-qt} \frac{SN(d1)σ}{2\sqrt{T}}+rKe^{-rt}N(-d2)-qSe^{-qt}N(-d1)$$
配当利回りqなし
$$セータ(call) = -\frac{SN(d1)σ}{2\sqrt{T}}-rKe^{-rt}N(d2)$$
$$セータ(put) = -\frac{SN(d1)σ}{2\sqrt{T}}+rKe^{-rt}N(-d2)$$
上の計算式のように、権利行使価格やSQ日が同じコールオプションとプットオプションでも、セータ値が異なります。
ただし、金利rと配当利回りqがともに0%のときは、コールオプションとプットオプションのセータは同じになります。
$$セータ(call,put) = -\frac{SN(d1)σ}{2\sqrt{T}}$$
グラフで見る!セータの見方【SQ日との関係】
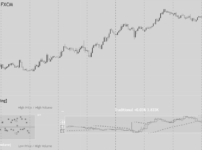
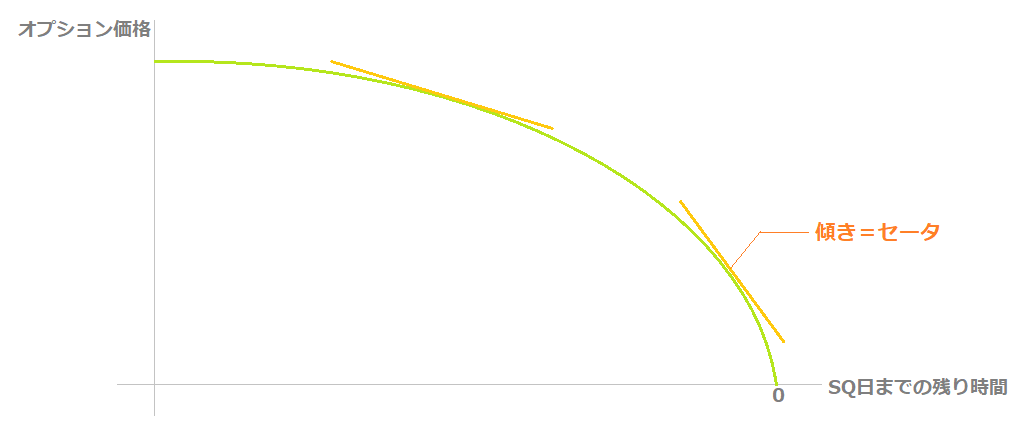
上でも述べましたが、セータは「オプション価格-SQ日までの残り時間」のグラフの傾きになります。
上の図は、ATMオプションのグラフで、SQ日が近づくほど傾き(=セータ)が大きくなっています。
セータ vs 権利行使価格
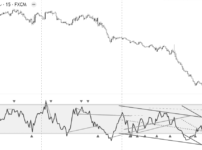
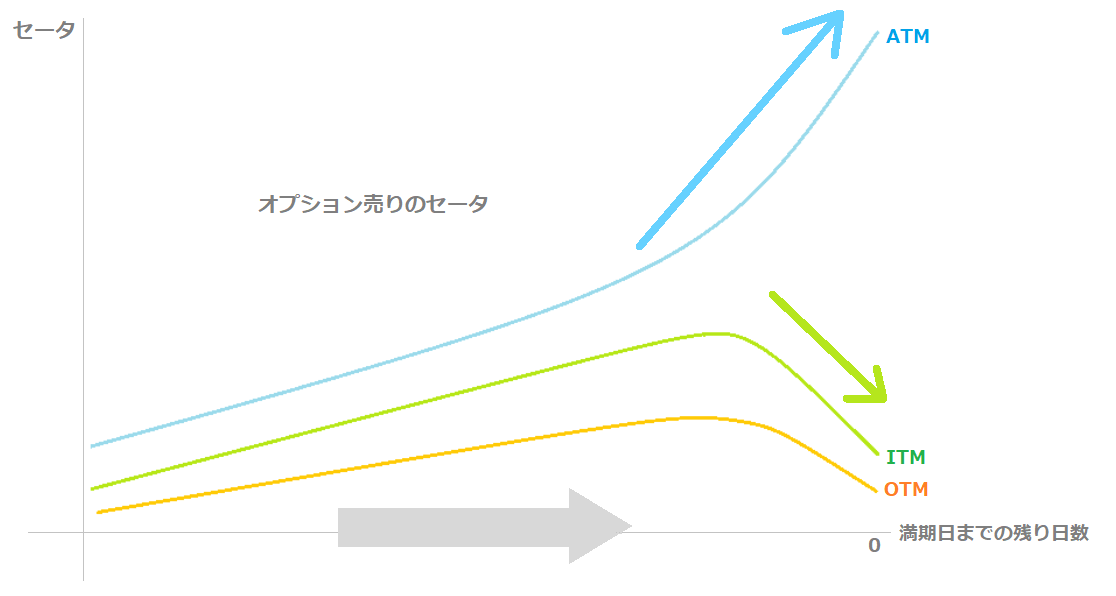
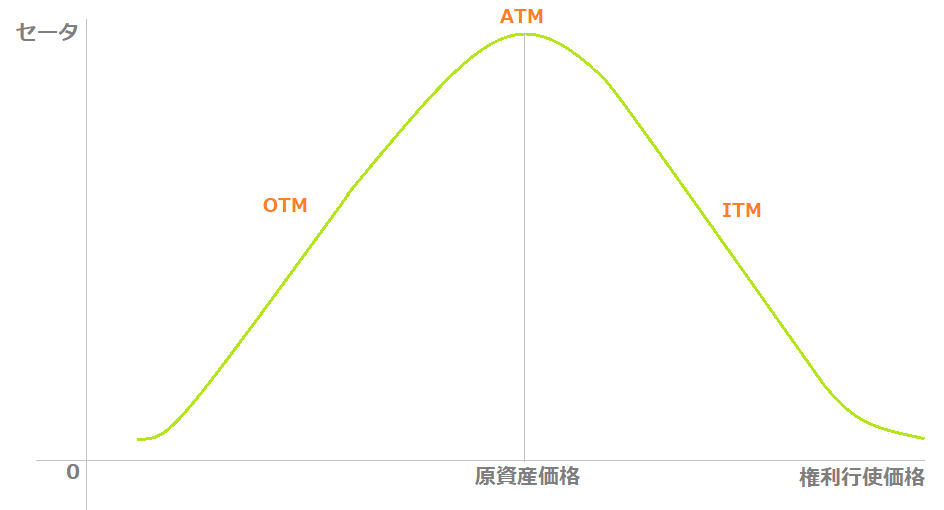
下の図は、オプション売りにおける「セータ-権利行使価格」のグラフです。
- ATMのセータは最大値をとり、ITMやOTMのセータより高い
- 権利行使価格が原資産価格から左右に離れるほど、セータは減少する
※深いITMやOTMのポジションの大部分は本質的価値で構成され、時間価値の減衰による影響を受けにくいため、セータは0に近い数値をとります。
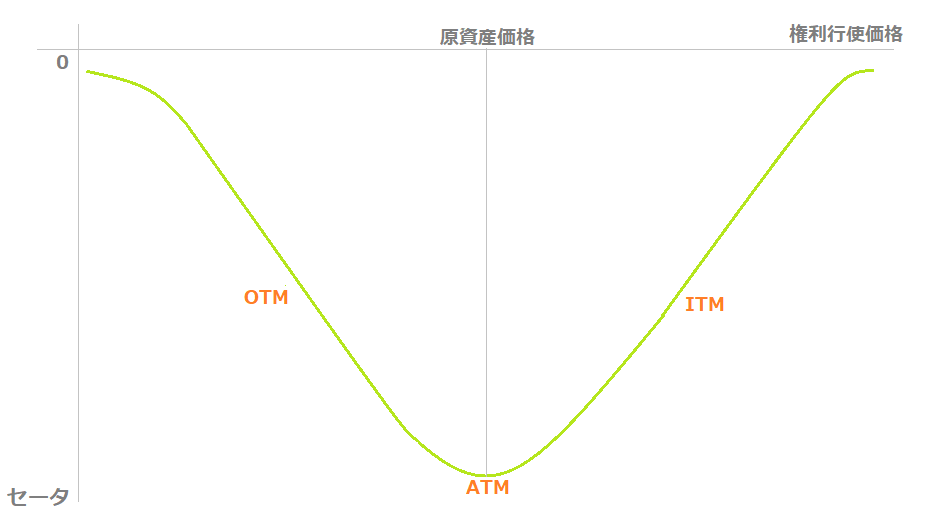
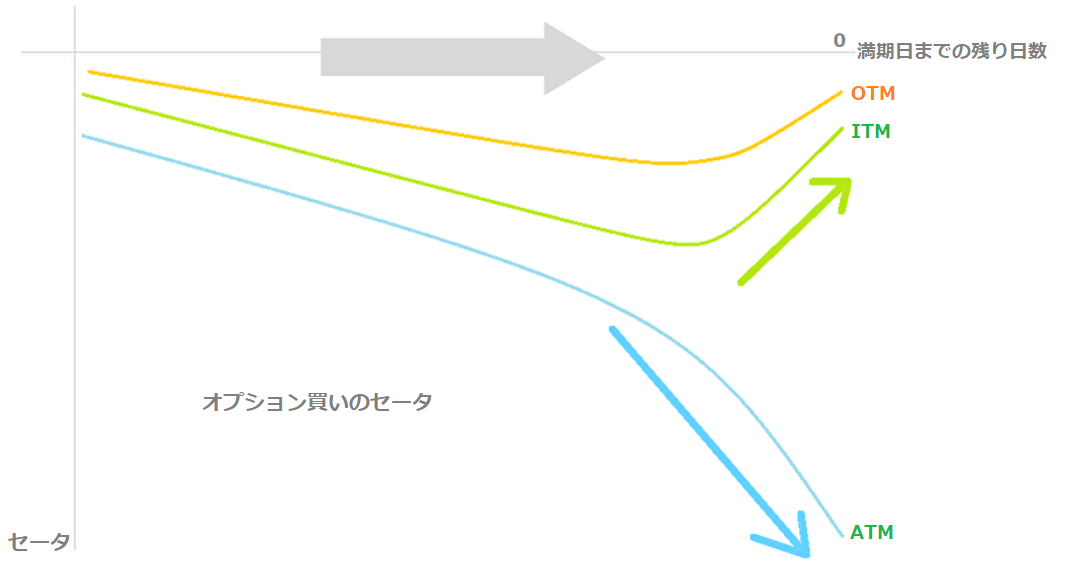
オプション買いのセータの場合、ATMで最小値をとり、ATMやOTMが深くなるほどセータは上昇します。
セータ vs オプションの残存期間
短期オプションは長期オプションに比べ、セータがOTM・ATM・ITMいずれも低くなります。
下のグラフは、満期日までの残り日数が1か月・2か月・3か月それぞれのセータを表します。
セータ vs 時間
オプション売りでは、満期日が近づくとATMのセータは急騰し、OTMやITMのセータは逆に減少します。
オプション買いでは、ATMのセータは急落し、OTMやITMのセータは0に向かって上昇します。
以上のように、セータ値は原資産価格や満期日までの残り日数に影響を受けます。
他に、インプライドボラティリティもセータの値に影響を与えます。
セータとインプライドボラテリティの関係
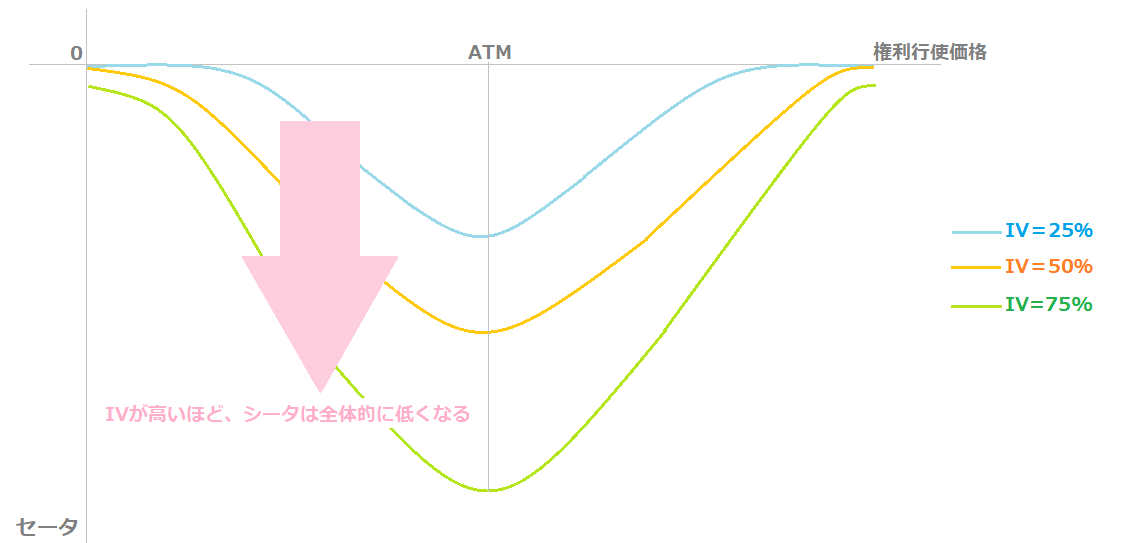
下の図は、IV=25%・50%・75%それぞれのコールオプション(SQ日同じ)の「セータ-権利行使価格」のグラフです。
インプライドボラティリティが変化しても、セータの全体的な形は変わりなく、ATMでセータは最小値となります。
また、IVが高いほど、セータの絶対値は大きく、低IVのオプションに比べてセータは全体的に低い数値をとります。
これは、IVが高いオプションほど、時間価値の減衰による影響が大きく、オプション価格が大きく下がりやすいことを示しています。
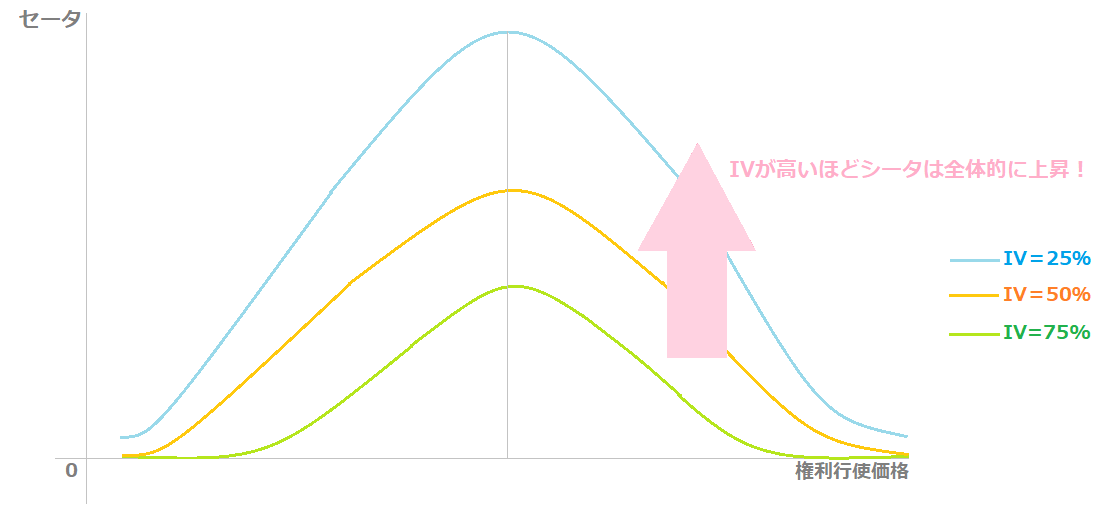
下の図は、IV=25%・50%・75%それぞれのプットオプションにおけるセータのグラフです。
プットオプションの場合は、IVが高いほどセータは全体的に上昇します。
セータを使ったオプション売り戦略
オプション売りは、時間価値の減衰から利益を得ることができる取引です。
時間価値の減衰 → オプション価値の下落 → オプションを安い価格で買い戻せる
オプション売りのコツ1
満期日まで残り1か月~数週間前にオプション売りを仕掛ける
満期日が近づくとセータ値は加速するため、時間価値の急落から利益を上げることができます。
また、このオプション売りで利益を上げるには、停滞している相場で仕掛けることが大切です。
原資産が不利な方向に動くと、損失が拡大する危険性があります。
オプション売りのコツ2
レンジ相場を形成している市場・時期にオプションを売る
セータを利用して、時間価値の減衰から利益を上げる戦略の1つに「クレジット・スプレッド」があります。
この戦略は、同じ原資産・SQ日のオプションにおいて、低価格のオプションを買い、高価格のオプションを売ります。
ポジション全体で正のセータとなるため、ダイム・ディケイの恩恵を受けることができます。
補足
複数のオプションを取引する場合は、合計セータの符号に注意しましょう。
・Σセータ=正:時間経過により、オプション全体でタイムディケイの恩恵を受ける
・Σセータ=負:時間経過により、オプション全体で時間価値の減衰から悪影響を受ける
そのため、時間価値の減衰の影響を受けたくないようヘッジしたい場合は、合計セータが0または正になるよう、プット売りまたはコール売りのポジション建てて合計セータを調整する必要があります。